Learning to Overtake in Drone Racing via Recurrent Reinforcement Learning

We study the problem of enabling an autonomous drone to overtake a leading opponent in head-to-head racing. While single-agent reinforcement learning with simple feedforward policies suffice for minimizing lap time, these policies fail in competitive settings due to their inability to anticipate opponent motion. We propose a recurrent architecture that stacks a two-layer LSTM and four-layer MLP and extends the ego drone's observation with the full opponent state and is trained with Proximal Policy Optimization. Our results show significant improvements in overtaking performance, with the recurrent policy consistently outperforming pure feed-forward architectures in competitive racing scenarios.

Introduction

Autonomous drone racing presents a challenging reinforcement learning (RL) problem due to the importance of real-time decision making and high-speed control in the presence of an opponent. In single-agent time trials in simulation, effective policies that minimize lap time can be learned using simple feedforward neural networks (FNNs) and model-free RL with full access to the agent's true state. However, when the domain is expanded to multiple agents, where drones must react to and overtake opponents, naive implementations of these policies tend to fail, despite extending the observation space to include opponents' states. We attribute this failure to the non-stationary transition dynamics of the environment and a lack of temporal reasoning, which restricts the policy's ability to recognize patterns in opponent behavior and pilot accordingly.

To address this problem, we explore the use of recurrent neural networks (RNNs) in the form of Long Short-Term Memory (LSTM) in head-to-head drone racing on a life-size figure 8 track. We fix the opponent drone's policy and train the ego drone to overtake. Our proposed method augments the ego drone's observation space to include the full state of the opponent drone, in contrast to the standard setup that only includes the opponent's relative position. The policy network is then structured as a two-layer LSTM followed by a four-layer multilayer perceptron (MLP), enabling the agent to capture temporal patterns in both the opponent's trajectory and its own motion. Our results indicate that the recurrent architecture enables the ego drone to learn to anticipate and exploit the opponent's behavior.

Contributions

• We show that pure-MLP policies that succeed in single-agent racing fail to perform in head-to-head racing despite fully observing the opponent state.
• We introduce an RNN-based architecture that improves overtaking behavior and demonstrate it in simulation.
• We include supplementary videos of the policies.

Background

On identical hardware, overtaking an opponent is oftentimes not a matter of achieving higher straight-line speed, but rather executing deliberate trajectories to surpass the opponent during turns. In motorsport, drivers are told to “carry more momentum” than the leading car when approaching an overtake. We define momentum as \( p = mv \). If two identical side-by-side vehicles approach a turn, the vehicle that maintains a greater forward velocity \( v \) through the turn exits with greater momentum \( p \), and therefore gains the positional advantage. The velocity, however, is constrained by its centripetal acceleration \( a_c \), as defined in (1):

\[ a_c = \frac{v^2}{r} \tag{1} \]

In motorsport, \( a_c \) is a function of the available lateral grip, typically modeled by a friction limit due to the track surface. In the context of drone racing, the same principles apply in three-dimensional space, only now with aerodynamic constraints that limit \( a_c \). From (1), it follows that maximizing the turn radius \( r \) allows for a higher cornering velocity \( v \). This motivates wide cornering lines for overtaking. A drone that can anticipate an opponent's future position will be better at selecting a wide or tight racing line that maximizes its exit speed and also avoids collisions.

Existing RL-based racing policies typically optimize only for minimizing lap time, and do not account for the presence of dynamic opponents. This is in part due to the implicit assumption in standard RL formulations that the transition dynamics of the underlying Markov Decision Process (MDP) are stationary:

\[ P(s' \mid s, a) \tag{2} \]

In other words, standard RL approaches that succeed in single-agent racing environments assume that the next state \( s' \) only depends on the current state \( s \) and the agent’s action \( a \), and not on another agent’s policy. The non-stationary nature of the environment in multi-agent drone racing leads to the failure of single-agent policies in head-to-head competition as they are unable to anticipate opponent behavior.

LSTMs, a type of RNN, are well-suited for learning in temporally correlated environments. Unlike MLPs, LSTMs maintain an internal memory that evolves over time, allowing them to capture patterns in sequential data. In multi-agent drone racing, this capacity allows the policy to track the opponent’s motion over time and implicitly reason about its future state; this leads to better policy updates.

Related Work

[Geles et al., 2024] show that end-to-end reinforcement learning from pixels enables agile drone flight, but their work focuses solely on single-agent time trials without opponent interaction. [Spica et al., 2018] address competitive drone racing through a game-theoretic planner, though their approach relies on model-based control and assumes full observability. [Werner et al., 2023] explore decentralized multi-agent learning for team-based racing, whereas our work focuses on two-agent competition using a recurrent policy to learn overtaking behavior against a fixed adversary. Hernandez-Leal et al. [2019] show that model-free approaches are more robust to dynamic opponents because they directly learn a policy without relying on incorrect environment models, though we show that a model-free approach alone is insufficient without temporal reasoning.

Approach

Our approach consists of a two-stage training pipeline designed to enable overtaking in drone racing using reinforcement learning. We first train a time-trial policy for a single drone to follow a figure-eight trajectory without any opponents. This policy is then frozen and fixed to the opponent in a head-to-head two-drone setup, where a second ego drone learns to anticipate and overtake the opponent. Both stages are trained using PPO, but differ in observation space, architecture, and reward structure.

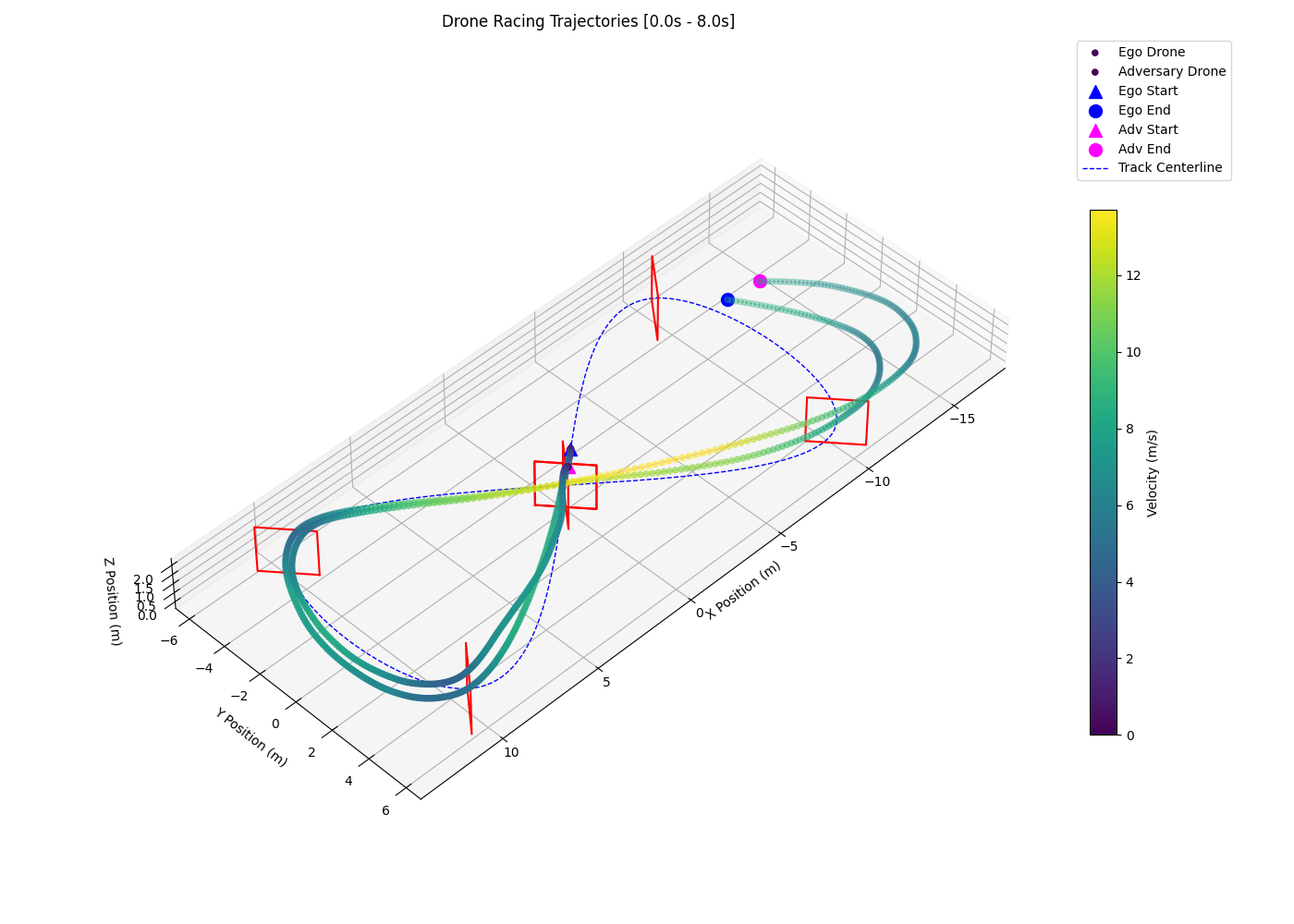
Stage 1: Single-Agent Time-Trial Policy. In the first stage of our training pipeline, we train a drone in a single-agent environment. The drone follows a 3D figure-eight trajectory by tracking a series of waypoints located at the center of each gate in a life-size drone racing track. We opt to use a life-size track to expose abilities that benefit from scale, such as reaching maximum speed in a straight, that are otherwise hidden in a scaled-down track. Conducting RL on a life-size track also exposes obstacles that arise from long-horizon tasks and emulates real-world robot learning.

The observation space consists of 17 features: relative position to the next gate in the gate frame (3-dim), quaternion (4-dim), body-frame linear velocity (3-dim), body-frame angular velocity (3-dim), and the previous control action (4-dim).

The policy is composed of a two-layer multilayer perceptron (MLP) with 128 hidden units per layer and utilizes tanh activations, outputting a value between -1 and 1. The action space \( \mathbf{A}_{\text{prop}} \in \mathbb{R}^4 \) is four-dimensional and maps the [-1, 1] output of the neural network \( \mathbf{A}_{\text{nn}} \in \mathbb{R}^4 \) to a propeller speed given by:

\[ A_{\text{prop}} = 14468.429 \cdot (1 + 0.8 A_{\text{nn}}) \tag{3} \]

We train the network using PPO and employ a clipped surrogate objective with the following hyperparameters: Clip parameter \( \epsilon = 0.2 \); Desired KL divergence: 0.01; Entropy coefficient: 0.01; Discount factor \( \gamma = 0.99 \); GAE parameter: \( \lambda = 0.95 \); Learning rate: \( 1 \times 10^{-4} \); Number of epochs per iteration: 5; Number of minibatches per epoch: 4. We simulate 8192 parallel environments and specify that each environment collects 100 timesteps of experience before a PPO update is performed; the operating frequency is 50 Hz so 100 timesteps corresponds to 2 seconds. We use a standard Actor-Critic PPO implementation from the RSL RL library by Rudin et al. [2022].

We use a dense reward to guide learning and encode the task of racing, inspired by Geles et al. [2024] and refined further through trial-and-error for our task. At each timestep, we compute the total reward \( r_t \) given by:

\[ r_t = r^{\text{prog}}_t + r^{\text{pass}}_t - r^{\text{cmd}}_t - r^{\text{crash}}_t \tag{4} \]

where the individual components are defined as:

\[ \begin{aligned} r^{\text{prog}}_t &= \lambda_1 (d_{t-1} - d_t) \\\\ r^{\text{cmd}}_t &= \lambda_2 \|a_t\| + \lambda_3 \|a_t - a_{t-1}\|^2 \\\\ r^{\text{pass}}_t &= \begin{cases} 1.0 - d_t & \text{if passing gate} \\\\ 0 & \text{otherwise} \end{cases} \\\\ r^{\text{crash}}_t &= \begin{cases} 5.0 & \text{if collision} \\\\ 0 & \text{otherwise} \end{cases} \end{aligned} \tag{5} \]

We use hyperparameters \( \lambda_1 = 0.5 \), \( \lambda_2 = 0.0005 \), and \( \lambda_3 = 0.0002 \).

Stage 2: Multi-Agent Overtaking Policy. In the second stage of our pipeline, we train a second drone (or ego drone) to race against the fixed opponent drone that executes the policy learned in Stage 1.

To enable overtaking behavior, the ego drone receives a 30-dimensional observation vector that includes both its own full state and the opponent’s full state. Specifically, we append to the existing observation vector from Stage 1 to include the opponent’s relative position to the ego in the ego frame (3-dim), opponent’s quaternion (4-dim), opponent’s ego-frame linear velocity (3-dim), and the opponent’s ego-frame angular velocity (3-dim).

The ego drone’s policy is trained using a recurrent Actor-Critic PPO implementation from the RSL RL library Rudin et al. [2022]. Both actor and critic networks share an identical architecture and 30-dimensional observation vector. We use a two-layer LSTM module with a hidden size of 128, followed by a four-layer MLP with dimensions 256, 128, 128, and 64. The architecture uses tanh activations and is initialized with an action noise standard deviation of 1.0 for early exploration. The hidden state of the LSTM allows the network to capture sequences in both the ego and opponent motion and thus learn effective trajectories that overtake the opponent.

Compared to the single-agent baseline, the recurrent architecture possesses a larger capacity and now incorporates memory through the LSTM hidden state. We decrease the learning rate from \( 1 \times 10^{-4} \) to \( 1 \times 10^{-5} \) and reduce the entropy coefficient from 0.01 to 0.008. The length of the temporal sequence processed by the LSTM is 100 timesteps long. We modify the rewards from Stage 1 (Equation 4) to include an additional component, the competition reward \( r^{\text{comp}}_t \). We attempt two different approaches to define the competition reward:

\[ r^{\text{comp}}_t = \tanh(-0.1 \cdot d_{\text{forward}}) \tag{6} \]

\[ r^{\text{comp}}_t = \begin{cases} 1.0 & \text{if ego is at target and ahead in gate index} \\ 0 & \text{otherwise} \end{cases} \tag{7} \]

Equation (6) encourages a constant forward lead over the opponent where \( d_{\text{forward}} \) is the relative distance from the ego drone to the opponent projected onto the ego’s forward axis. Equation (7) encourages a discrete binary lead by rewarding the ego with a fixed reward of 1.0 when it has both crossed the plane of a gate and maintains a higher current gate index than the adversary. In this project we attempt both reward structures, but progress further with the dense reward (6). We retain the sparse reward (7) for potential ablation studies.

Results

We now evaluate the efficacy of our two-stage training pipeline in Table 1 with (i) the success rate, averaging the number of gates the ego (or single-agent) drone passes over the total number of gates encountered over 45 seconds, (ii) the crash rate, averaging the number of episode resets due to collision over 45 seconds, (iii) the fastest lap-time, and (iv) the overtake rate, averaging the number of times the ego sustains a positional advantage after making an overtake. If the drone does not learn to overtake at all, it is denoted with ’Fail’.

Comparison of Policy Architectures

Policy	Success Rate	Crash Rate	Lap Time (s)	Sustained Overtake Rate
(A) Single-Agent 2-layer MLP (17-dim input)	0.975 (39/40)	0.02	6.92	--
(B) 2-layer MLP (20-dim input)	0.517 (15/29)	0.31	DNF	Fail
(C) 4-layer MLP	0.621 (18/29)	0.24	DNF	Fail
(D) 4-layer MLP (Sparse rcomp)	0.588 (20/34)	0.31	DNF	Fail
(E) 1-layer LSTM w/ 4-layer MLP	0.571 (12/21)	0.22	DNF	Fail
(F) 2-layer LSTM w/ 3-layer MLP	0.535 (23/43)	0.49	DNF	0.33 (2/6)
(G) 2-layer LSTM w/ 4-layer MLP	0.857 (30/35)	0.18	7.65	0.50 (4/8)

Table 1: Quantitative evaluation of single-agent and multi-agent policies. All policies use a 30-dimensional observa- tion vector as input unless otherwise specified—the 20-dim input for policy (2) appends a 3-dimensional xyz relative position of the opponent in ego frame. All multi-agent policies use the dense reward competition defined by (6).

Among the multi-agent policies evaluated, the 2-layer LSTM with 4-layer MLP architecture achieves the strongest performance across all metrics. It not only exhibits the highest success rate (0.857) and lowest crash rate (0.18), but also demonstrates the ability to consistently complete laps and perform sustained overtakes—maintaining a positional advantage in 4 out of 8 attempts. In contrast, the pure MLP policies either crash frequently or fail to complete a lap, and all are unable to perform any overtakes, indicated by the “Fail” entries in the final column. Most importantly, all of the pure MLP policies demonstrate a total inability to fly with opponent observations as policy inputs. In fact, we find that the highest performing pure MLP policy, policy (C), is able to fly smoothest when within the proximity of the opponent, and when the opponent accelerates away from the ego drone in the straights, the ego’s loses control as shown in Figure 2. We also note that the ego drone with policy (C) refuses to fly past and overtake the opponent, despite clear opportunities to do so. This is likely because the bulk of its replay buffer consists of trajectories where it remains behind, and this causes the policy to overfit to trailing behavior without discovering any overtaking actions. It is possible that this behavior could be combated by training the ego policy using self-play, so that the opponent drone does not dominate the race in early training. Training via self-play would provide instances during the exploration stage where the ego may have a positive forward lead due to the opponent’s policy outputting equally arbitrary motor commands; this could allow for the ego drone to discover overtaking despite having no temporal memory. In our specific training pipeline, however, we show that lacking temporal memory prevents the pure MLP policies from acting effectively on opponent observations.

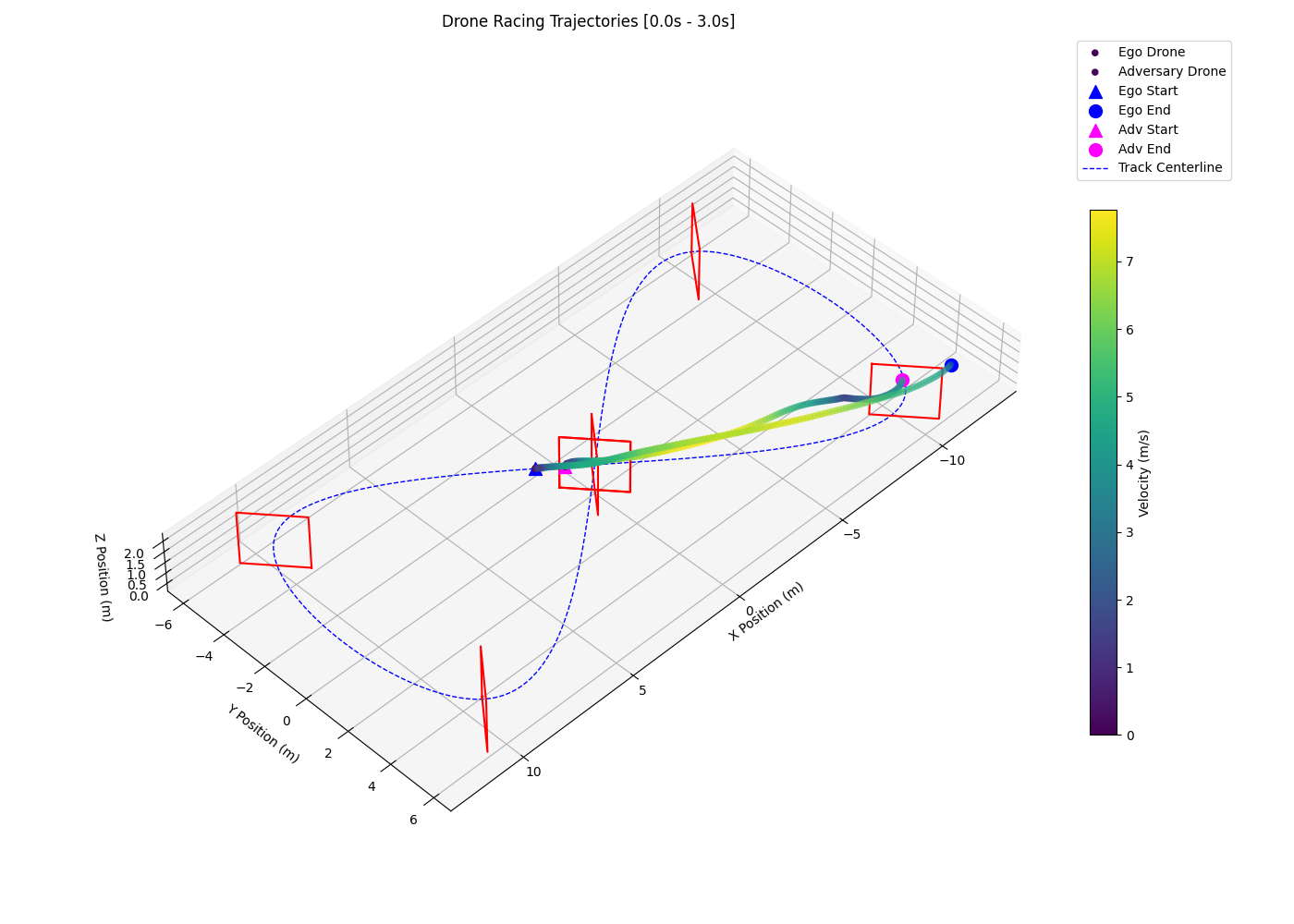
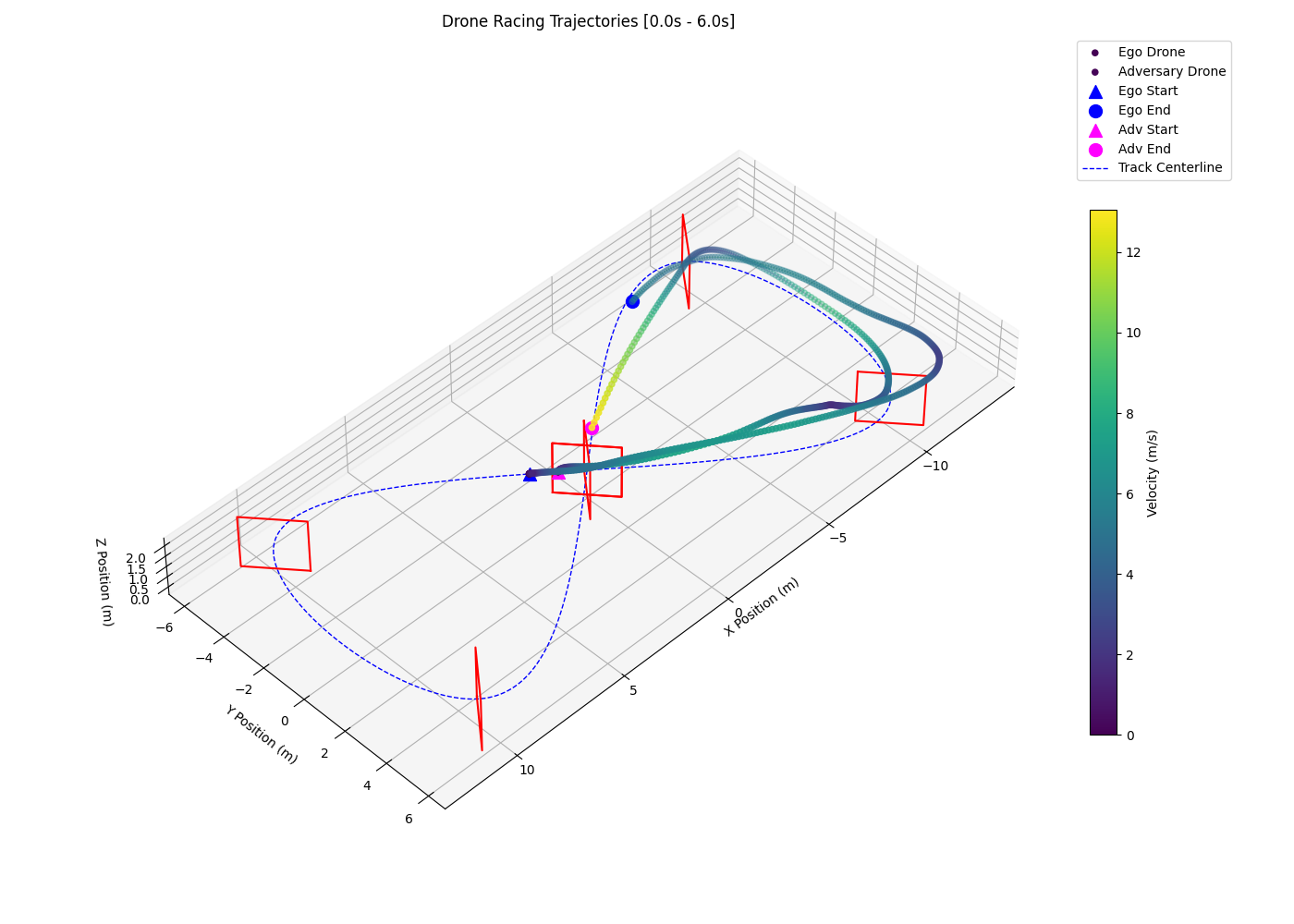
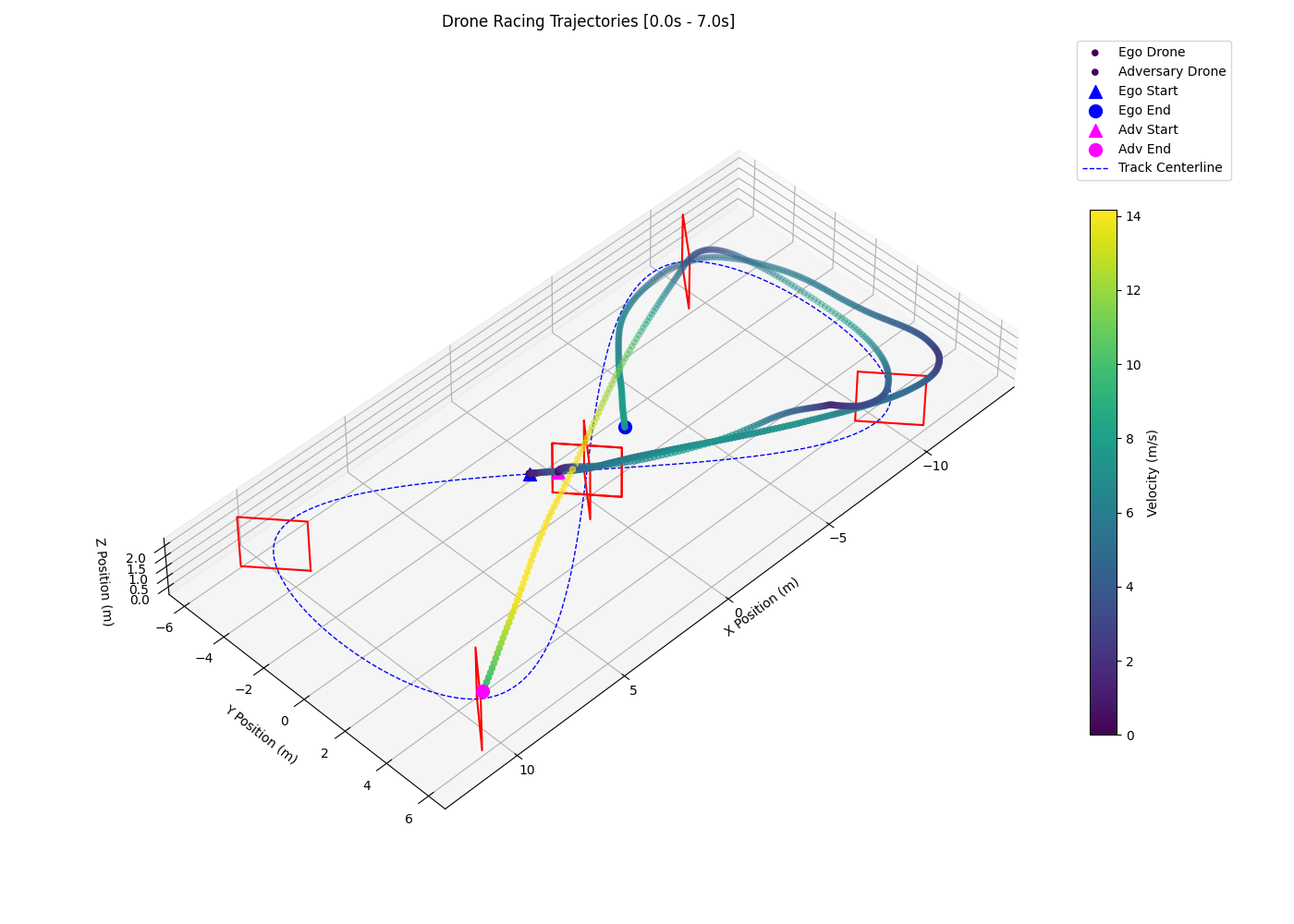
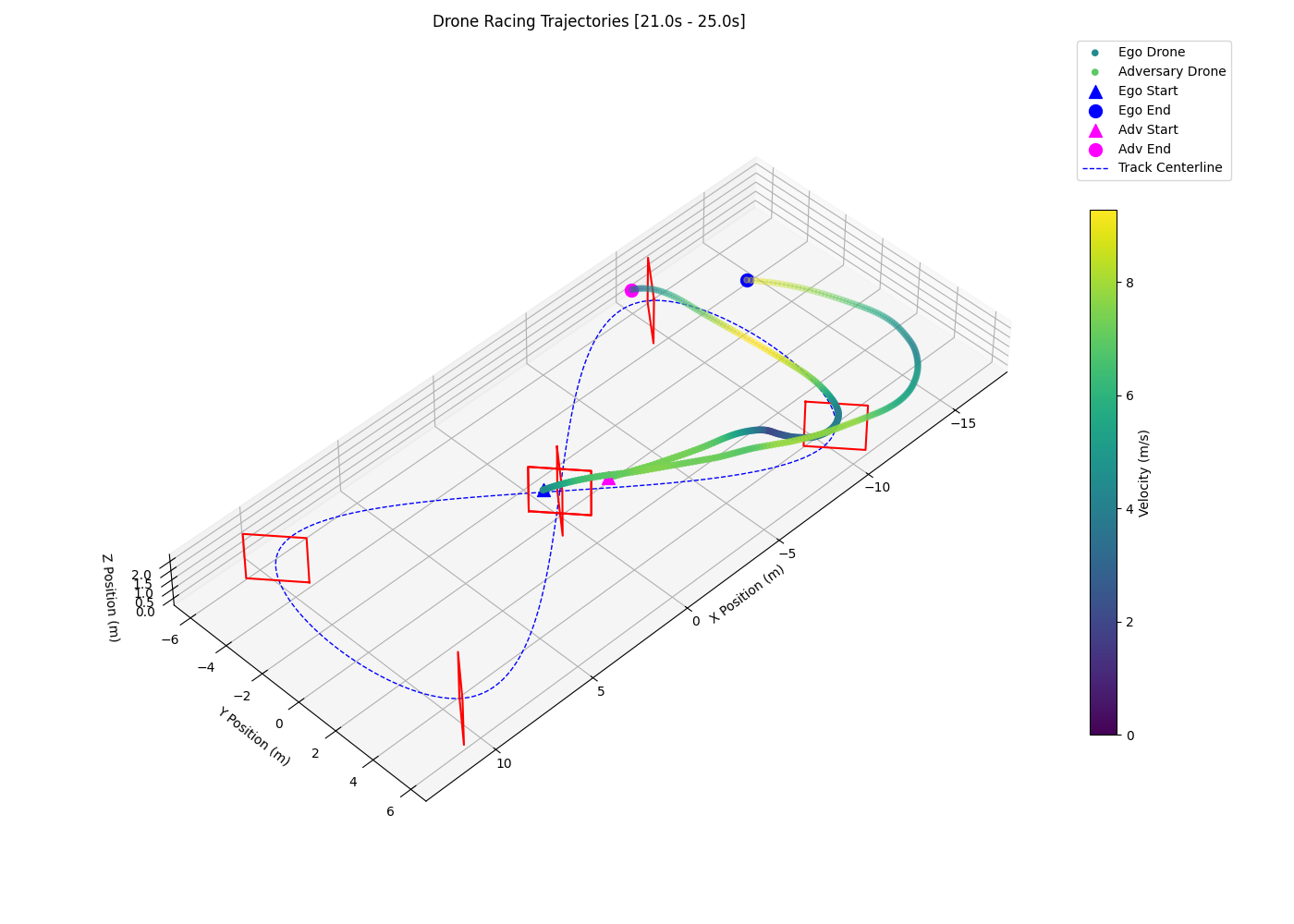
Interestingly, the 2-layer LSTM with 3-layer MLP policy (F) shows signs of opponent anticipation by entering corners on a wide racing line. As shown in the left plot of Figure 3, the policy tends to prolong its wide racing line and regularly overshoots the following gate, losing the positional advantage and triggering the episode reset/collision condition which results in a high crash rate (0.49) and a low sustained overtake rate (0.33). The 2-layer LSTM with 4-layer MLP policy (G) successfully anticipates and overtakes the opponent by entering corners on a wide racing line and exiting on a tight and fast racing line, as seen in the right plot of Figure 3.

Discussion

We show through head-to-head drone racing that competitive multi-agent RL environments require more than simply extending the observation space or increasing network capacity. The failure of pure MLP policies to learn overtaking behavior despite having full access to the opponent state suggests that temporal reasoning is essential for producing competitive policies against dynamic opponents. Recurrent policies, such as the LSTM-MLP hybrid architecture we propose, are able to leverage sequential data to anticipate and exploit suboptimal opponent trajectories. We best demonstrate this observation by conducting successful overtakes in cornering scenarios.

The progression of our experiments also indicate that pure MLP policies appear to overfit to trailing behavior, likely due to the replay buffer being saturated with trailing examples due to opponent ability. Future work could explore curriculum learning or self-play to gradually increase the opponent ability and expose the ego drone to a wider variety of situations.

While we shaped our final policy with a dense competition reward, the sparse competition reward may still offer advantages. Future work could explore this reward to encourage longer-term planning and potentially allow for tactical behavior that sacrifices existing racing lines for more favorable future racing lines.

References

1. Ismail Geles, Leonard Bauersfeld, Angel Romero, Jiaxu Xing, and Davide Scaramuzza. Demonstrating Agile Flight from Pixels without State Estimation, 2024.
2. Pablo Hernandez-Leal, Bilal Kartal, and Matthew E. Taylor. A Survey and Critique of Multiagent Deep Reinforcement Learning. Autonomous Agents and Multi-Agent Systems, 33(6):750–797, October 2019.
3. Nikita Rudin, David Hoeller, Philipp Reist, and Marco Hutter. Learning to Walk in Minutes Using Massively Parallel Deep Reinforcement Learning. In Proceedings of the 5th Conference on Robot Learning, PMLR, 2022.
4. Riccardo Spica, Davide Falanga, Eric Cristofalo, Eduardo Montijano, Davide Scaramuzza, and Mac Schwager. A Real-Time Game Theoretic Planner for Autonomous Two-Player Drone Racing, 2018.
5. Peter Werner, Tim Seyde, Paul Drews, Thomas Matrai Balch, Igor Gilitschenski, Wilko Schwarting, Guy Rosman, Sertac Karaman, and Daniela Rus. Dynamic Multi-Team Racing: Competitive Driving on 1/10-th Scale Vehicles via Learning in Simulation. In Proceedings of the 7th Conference on Robot Learning, PMLR, November 2023.