Authors: Vineet Pasumarti, Ethan Senatore

The fast-paced and dynamic nature of racing provides an excellent platform to test different RL approaches. We identified this domain not only as an exciting application area but also as a practical environment with quantifiable metrics for testing the limits of RL algorithms. The challenge of pushing a robotic system to perform at high speeds while maintaining safety and precision peaked our curiosity and led to the development of this project. Both RL and IL have emerged in literature as feasible and competitive methods to solving the autonomous racing challenge. [1] End-to-end reinforcement learning agents have even shown impressive capabilities in new settings which allows for generalizable neural networks to have an adaptive racing policy [2]. We pose the question - can RL improve upon an IL policy to produce more robust and agile control policies that outperform the existing expert?
To investigate this, we chose the F1TENTH platform as our experimental testbed. Its scaled-down format supported by a lightweight simulator offer a preferable setting to evaluate and train different learning strategies. Ultimately, our goal is to better understand the trade-offs between imitation learning and reinforcement learning in the context of autonomous racing. In doing so, we wished to contribute insights into how these techniques can be combined to push the boundaries of autonomous driving performance.
End-to-end reinforcement learning approaches for autonomous racing have emerged as a successful strategy to surpass expert-level performance, [3] even outperforming human experts in certain domains like drone racing. There are far fewer studies that explore imitation learning for autonomous racing. This is for good reason. Reinforcement learning by nature improves its policy through 'reward hacking' and maximizes cumulative rewards, allowing for impressive performance in racing environments. [4] Imitation learning, however, typically reaches a performance ceiling determined by the capabilities of the expert policy. We assert that the performance of the policy can be improved upon by finetuning the weights of the IL neural network using on-policy reinforcement learning, such as Proximal Policy Optimization.
The most naive implementation of imitation learning is Behavior Cloning (BC). Behavior cloning uses supervised machine learning to map observations of the state space to actions, thus training the agent to learn an expert demonstrator's policy. BC, however, produces policies that are prone to experiencing a distribution shift, as the actions of the agent eventually shift its observations to be dissimilar from the expert data it was trained on.
Dataset aggregation (DAGGER) mitigates the effects of distribution shift by stochastically alternating control between the agent's policy and the expert policy to collect corrective labels. [5] While DAGGER reduces the compounding error issues of BC, it lacks strong convergence guarantees in general settings [6]. Human-Gated DAGGER (HG-DAGGER) refines this by letting a human expert serve as a gating function [7]. The agent executes actions until the human deems the state suboptimal and intervenes, at which point only the expert's actions are recorded. In practice, we can define a performance threshold to automate the human intervention. Existing work from Sun et al. [7] demonstrates that HG-DAGGER is a viable and tested imitation learning algorithm for F1TENTH autonomous racing.
Bootstrapping a PPO policy using HG-DAGGER presents a tractable method for autonomous vehicle control and an opportunity to outperform expert demonstrators. Because end-to-end RL approaches suffer from sample inefficiency when faced with high-dimensional action spaces that optimize both steering and speed, strategically decomposing the action space by mapping LiDAR observations to steering angle during the IL bootstrap, and exploiting higher speed during RL, the final policy may converge to outperform the expert demonstrations and/or exhibit superior performance than an end-to-end solution.
- We develop an IL-RL pipeline to surpass the performance of an expert demonstration.
- We provide a comparison of end-to-end RL policies and bootstrapped RL policies for racing.
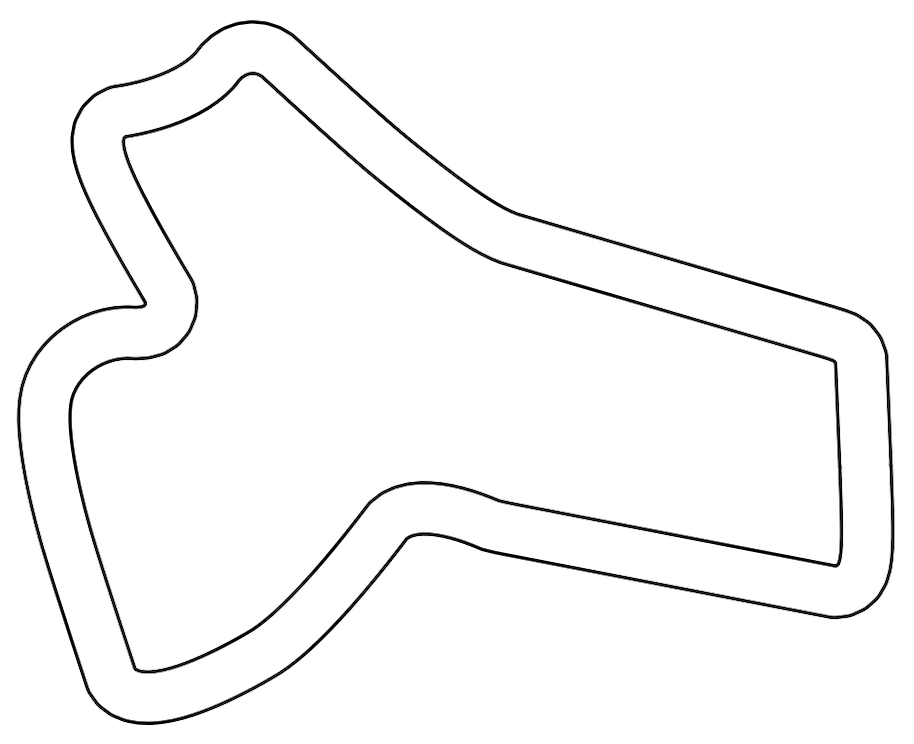
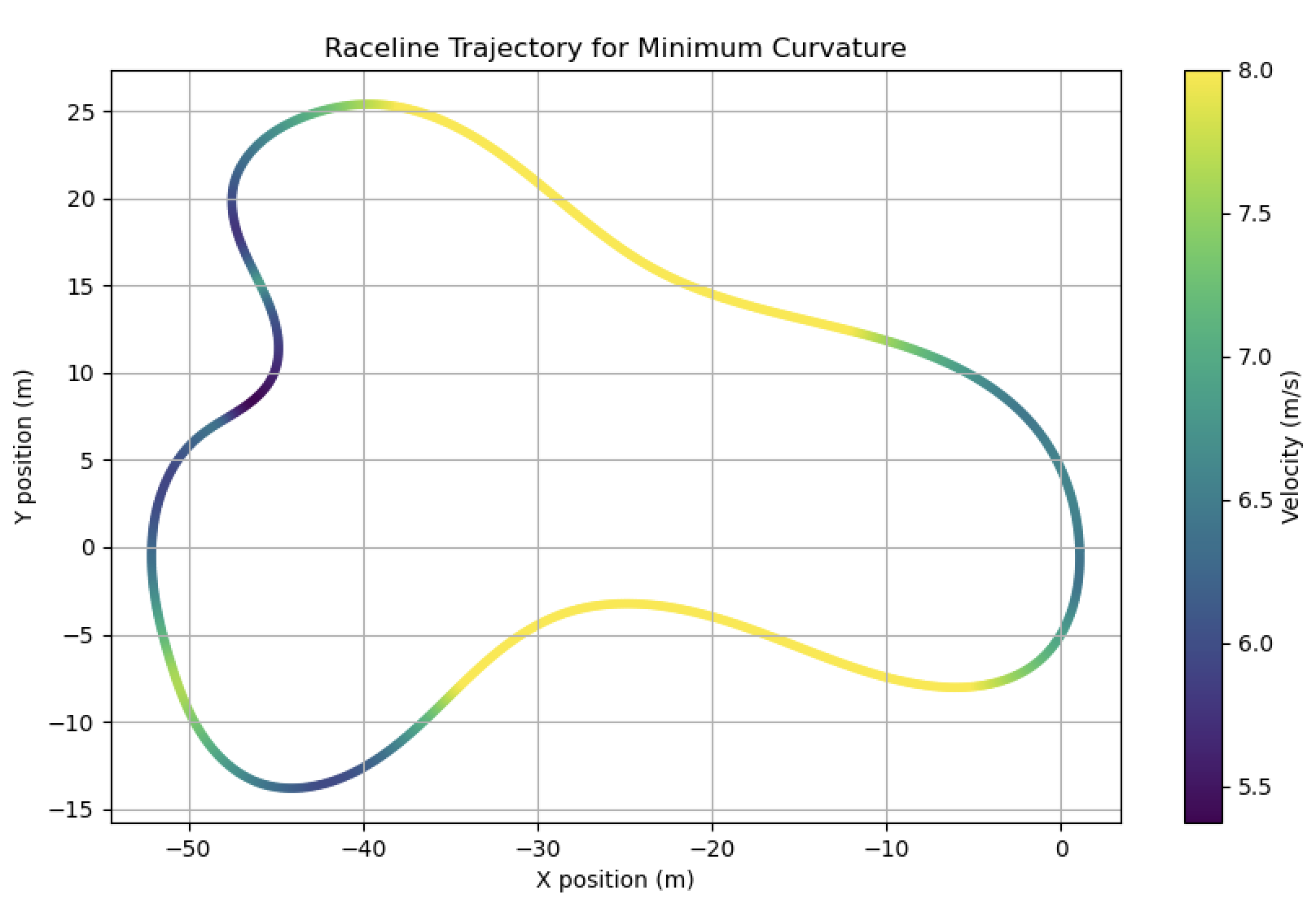
Fig. 1. (Left) The F1TENTH racetrack used for training and evaluation of the learned policies against expert demonstrations. (Right) The optimal raceline computed for minimum curvature and followed by the expert policy using a pure pursuit controller.
The agent's policy network is pre-trained using HG-DAGGER and finetuned with Proximal Policy Optimization (PPO) on a sample racetrack depicted in Figure 1. We repeat this process for each difficulty of expert demonstrations (easy, medium, hard) to produce three policies that are evaluated against the respective expert on the same racetrack that the policy is trained on.
We produce the learned policy inside the F1TENTH gym using HG-DAGGER for imitation learning. The expert demonstrations follow a classical pure-pursuit controller on an optimal raceline trajectory according to three different velocity profiles to represent three levels of difficulty. The learned policy is a multi-layer perceptron (MLP) that observes a 54-dimensional, down-sampled 1080-ray LiDAR scan concatenated with the car's current linear velocity. The hidden dimension is 256 and the learning rate is 0.0001. The pure-pursuit expert computes its control outputs using only the vehicle's (x, y) position and heading θ. The action space is continuous steering and speed for both policies.
We define three expert policies as an easy, medium, and hard demonstrator. For the easy and medium experts, we decouple the action space and fix their velocities at 3 m/s and 5 m/s respectively. The pure-pursuit controller outputs steering angle in accordance with an optimal raceline trajectory that is calculated by minimizing the summed curvature of the track and maintains a maximum top speed of 8 m/s [8]. The hard expert follows the longitudinal velocity (vx) and longitudinal acceleration (ax) profiles of the optimal raceline trajectory, reaching a top speed of 8 m/s in straights and maintains a minimum velocity of approximately 5 m/s in turns.
Human-gated imitation learning combats distribution shift by invoking the expert policy in unknown states. We define two thresholds, γv and γω, which equal 1 and 0.1 respectively. The expert policy is triggered during training when the difference in speed or steering angle between agent and expert has a magnitude greater than the prescribed threshold.
We employ Proximal Policy Optimization (PPO) to finetune the weights of the pre-trained HG-DAGGER imitation learning policy. The RL policy network utilizes an identical architecture as the IL policy, maintaining a 54-dimensional down-sampled LiDAR scan concatenated with the vehicle's linear velocity, and produces continuous steering and speed commands as outputs. We import weights from the HG-DAGGER policy network to initialize weights for the PPO policy network. We experiment with both an identical transfer of all weights in the network as well as specifically copying the feature extraction layers and steering output weight while randomly initializing the velocity input weight and speed output weight to encourage exploration.
The agent aims to maximize its cumulative rewards that track raceline progress, incentivize high velocity, and penalize collisions. We structure our rewards as the following:
where the individual components are defined as:
where vt is the current forward velocity at time t, which encourages the agent to maintain a high speed, Δst = st - st-1 represents the distance traveled along the track centerline since the previous timestep, and Rc indicates a collision penalty of -1.
During training, the PPO agent interacts with the environment and collects experience tuples (s, a, r, s', log π(a|s), done) to inform policy updates:
- State (s): The current observation (54-dimensional LiDAR scan + vehicle velocity) that serves as input to the policy network.
- Action (a): Steering angle and speed commands.
- Reward (r): Cumulative rewards as defined above.
- Next state (s'): Resulting observation after executing action a that is used to estimate the value function and calculate the advantage.
- Log probability (log π(a|s)): The likelihood of an action under the current policy.
- Done flag: Signals episode termination.
Our PPO implementation collects experiences in trajectories of 2048 steps before performing policy updates. We employ Generalized Advantage Estimation (GAE) with λ=0.95 to balance bias-variance tradeoff in advantage calculations. Policy optimization occurs over 10 epochs with actor and critic learning rates of 0.0002. We use mini-batches of size 64 and L2 regularization with coefficient 0.001. We apply a discount factor γ = 0.99 and constrain the policy update with a clip parameter ε = 0.2. We define the entropy coefficient and its decay as 0.001 and 0.99 respectively.
In our end-to-end reinforcement learning implementation, we maintain identical hyperparameters as the bootstrapped policy but randomly initialize all weights in the MLP for training.
Policy evaluation occurs at regular intervals, measuring average rewards and velocities across multiple episodes without exploration noise to monitor learning progress.
We evaluate the performance of the bootstrapped reinforcement learning policies against their respective expert policies of varying difficulty levels (Easy, Medium, Hard), as seen in Figure 2. We include a comparison of an end-to-end RL policy as well. Our performance metric is lap time where lower times indicate better performance.
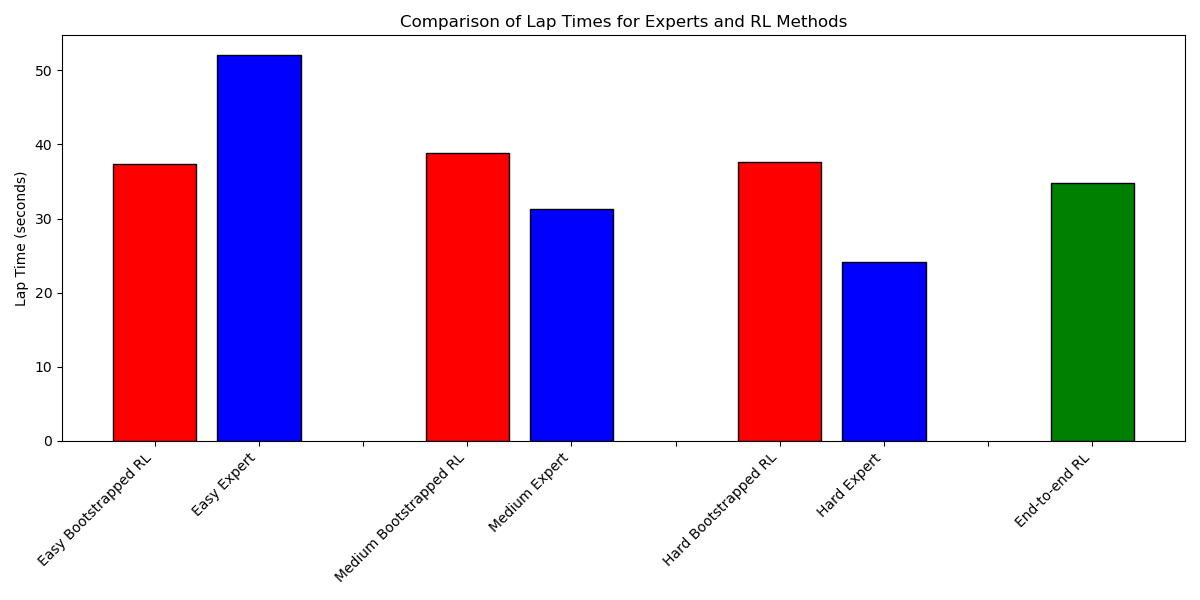
Fig. 2. Comparison of lap times for expert demonstrators and RL agents. The bootstrapped RL agents show similar performance and are outperformed by the end-to-end RL agent. Only the easy expert demonstrator is surpassed by the RL agents.
The Easy Bootstrapped RL agent (37.41s) significantly outperforms its corresponding Easy Expert demonstrator (52.12s), achieving a 28.22% reduction in lap time. This indicates that the learned policy successfully decouples the action space to learn the correct steering angles based on LiDAR scan and increase speed beyond the expert demonstrations to maximize cumulative rewards.
The Medium and Hard bootstrapped RL agents fail to outperform their corresponding expert demonstrations. The Medium Expert achieves a lap time of 31.27 seconds, outperforming the Medium Bootstrapped RL agent at 38.80 seconds. Similarly, the Hard Expert significantly outperforms the Hard Bootstrapped RL agent, with lap times of 24.11 seconds and 37.68 seconds respectively. We note that the performance gap between the expert and the bootstrapped RL agent widens as expert quality improves. Despite being provided a pre-trained policy equivalent to the expert, our results indicate that bootstrapped RL methods may struggle to match increasingly agile demonstrations in the context of autonomous racing.
We also recognize that all three bootstrapped policies achieved similar lap times (37.41–38.80s) despite being pre-trained by three different expert demonstrators of varying performance. This indicates that our PPO implementation likely plateaus in performance due to the reward structure and exploration parameters rather than by the performance of the imitation learning policy.
Interestingly, the End-to-end RL policy (34.75s), which was trained without imitation learning bootstrapping, outperformed all bootstrapped approaches although it still fell short of outperforming the Medium and Hard experts. The end-to-end RL agent's similarity in lap time to the bootstrapped agents also indicates the influence, or lack thereof, of the bootstrapped imitation learning policy on the final performance. The importance of the RL reward structure and exploration parameters strongly outweigh the importance of the bootstrap.
TABLE I
EXAMPLE MAP TESTING ACROSS DIFFERENT POLICIES
| Policy | Average Speed (m/s) | Average Lap Time (s) |
|---|---|---|
| Hard Expert | 6.48 | 24.11 |
| Medium Expert | 5.01 | 31.27 |
| Easy Expert | 3.14 | 52.19 |
| Hard Bootstrap RL | 4.15 | 37.67 |
| Medium Bootstrap RL | 4.03 | 38.79 |
| Easy Bootstrap RL | 4.18 | 37.41 |
| End-To-End RL | 4.50 | 34.75 |
We also note in Table I that the RL agents converge to a constant velocity that is maintained throughout the track, rather than vary velocity to achieve higher speeds in straightaways and maintain safe control during turns, as the hard expert does. A deeper neural network may learn this behavior, however, the 2-hidden-layer MLP utilized in our PPO implementation converges to a uniform velocity profile.
Although the IL bootstrap appears not to provide a lap time performance benefit compared to end-to-end RL, we record significantly better sample efficiency, as the bootstrapped RL policy converges at approximately 180,000 steps, compared to the end-to-end RL policy which converges at 500,000 steps.
For our end-to-end RL policy, finding a balance of the weights for each reward proved to be the most significant hurdle to overcome to achieve good performance. Each time a model was trained, we carefully noted how the policy behaved and whether it was able to strike a balance between speed and safety. We found that the average reward per episode, average episode length, and loss throughout training were the most helpful metrics to track to optimize performance. Additionally, we experimented with various amounts of training time steps to find when the policy converged to the best state. Ultimately, we found that ~500,000 time steps was sufficient for the policy to converge. Figure 3 depicts the average reward per step and average episode length per step for eight different training runs that we went through. Each policy had its strengths and weaknesses, and through careful experimentation we settled on the reward structure and weights mentioned in Equation (1). Each policy was trained on the example map depicted in Figure 1 which proved to be the most well-balanced track providing both long straights and sharp turns to train the policy.
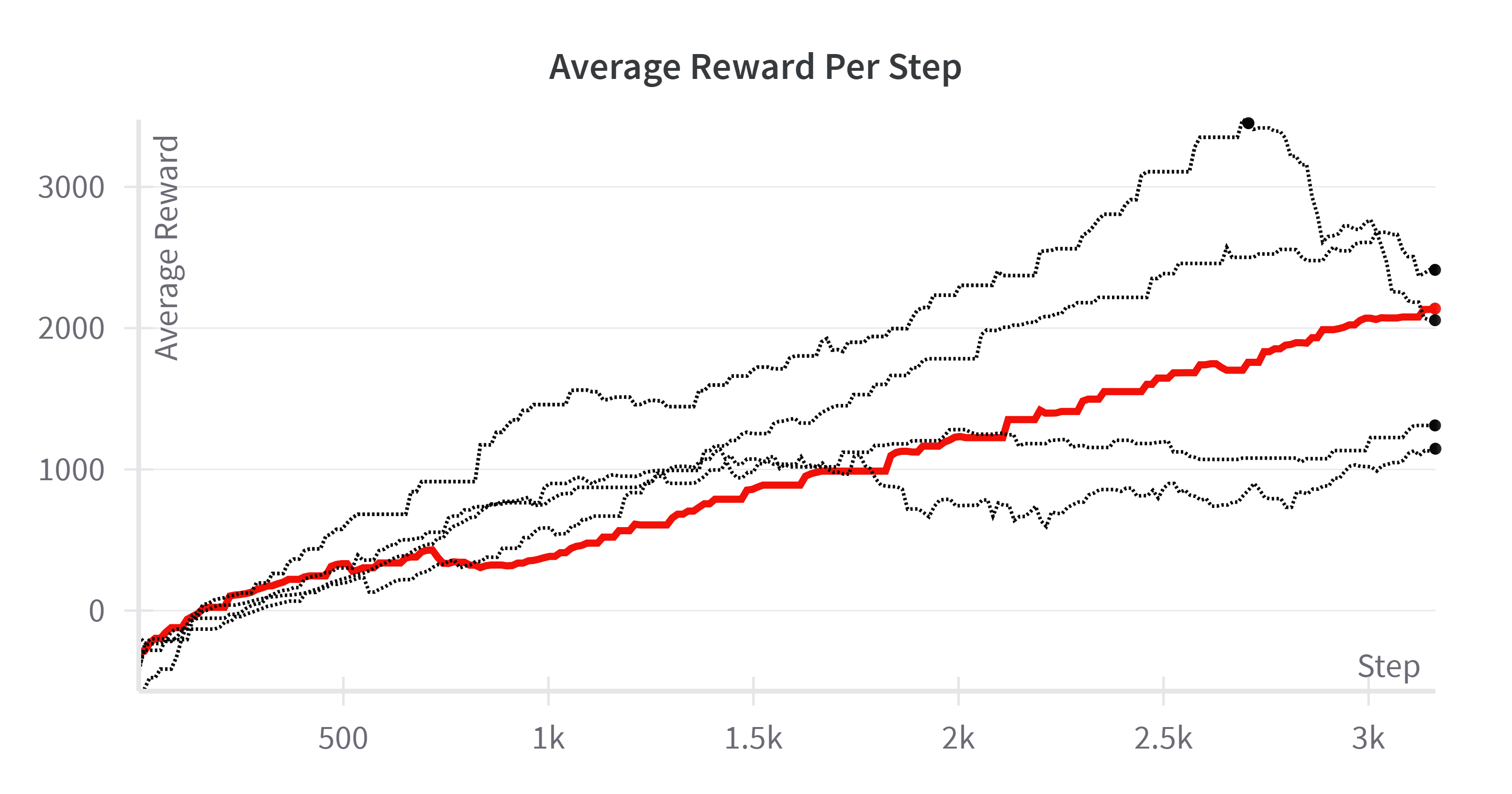
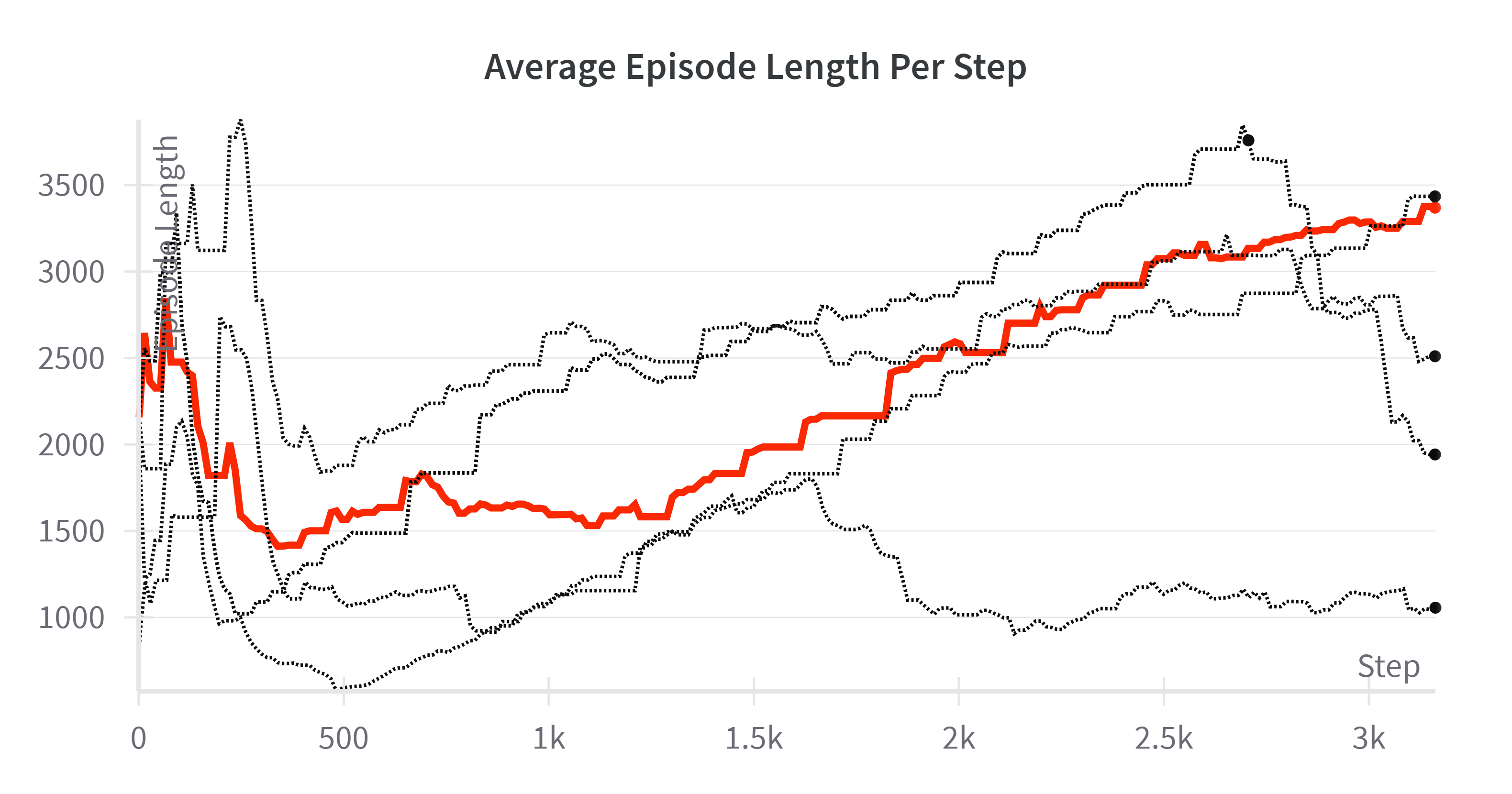
Fig. 3. (Left) The average reward per training step of eight different policies trained each with a unique reward structure. (Right) The average episode length per training step. The red line is the policy we settled with.
The end-to-end RL policy also proved to be successful in generalizing to different tracks. Due to the nature of the observations provided to the policy, no map is memorized. In contrast, the agent is able to adapt to various tracks and simply react to differing scans of its environment. Table II presents the performance of the End-to-End RL policy across a diverse set of one-tenth sized real-world tracks. Overall, the policy demonstrates a commendable degree of generalization, managing to complete full laps on the majority of tracks despite being trained on a single map.
TABLE II
END-TO-END RL TEST METRICS ACROSS DIFFERENT
TRACKS (25 LAPS EACH)
| Track | Average Speed (m/s) | Average Lap Time (s) | Lap Completion (%) |
|---|---|---|---|
| Example Map | 4.50 | 34.75 | 100 |
| Spielberg | 4.46 | 78.64 | 100 |
| Nuerburgring | 4.21 | 112.42 | 84 |
| Sao Paulo | 4.33 | 85.27 | 96 |
| Spa | 4.83 | 116.32 | 12 |
| Hockenheim | 4.85 | 81.63 | 8 |
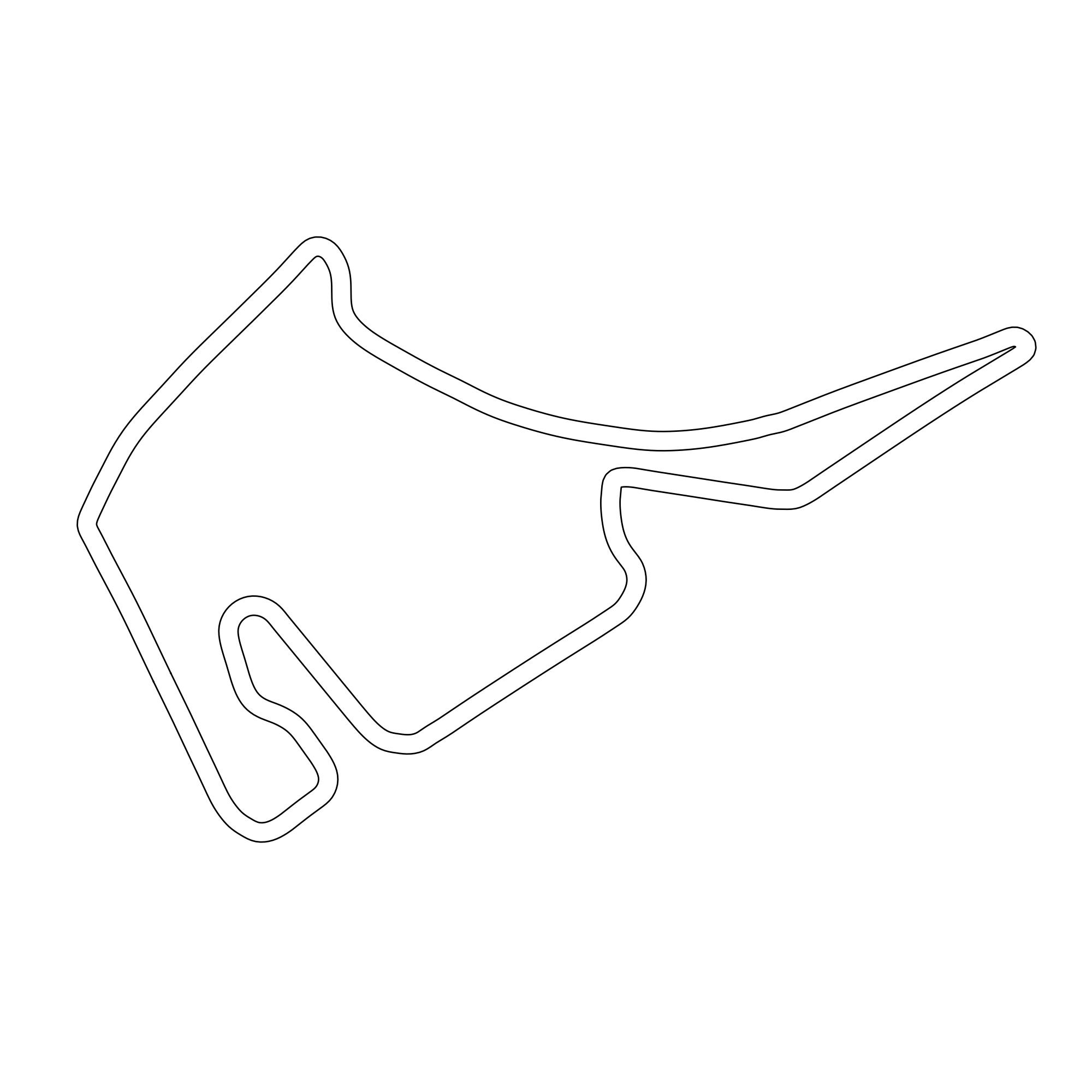
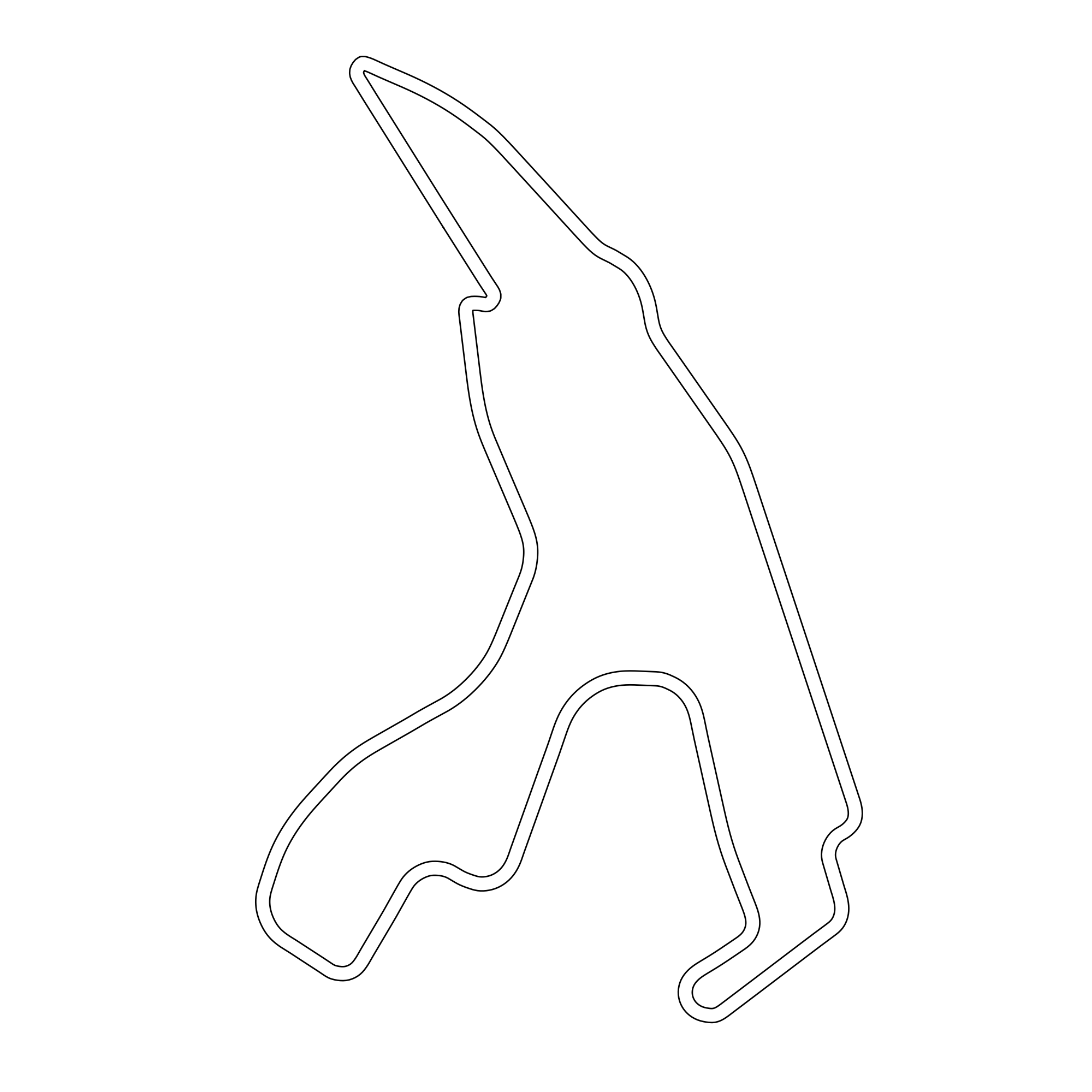
Fig. 4. (Left) Hockenheim. (Right) Spa-Francorchamps.
The Example Map, which the policy was trained on, yields optimal results with 100% lap completion, a moderate average speed (4.50 m/s), and a short lap time (34.75 s). On more complex circuits like Spielberg and Sao Paulo, the policy still performs reliably, maintaining high completion rates (100% and 96%, respectively), although lap times increase, indicating out-of-distribution curvature that forces more cautious navigation and suboptimal trajectories. However, the agent's limitations become evident on tracks like Nuerburgring, Spa-Francorchamps, and Hockenheim. Although it retains respectable speed (over 4.2 m/s in all cases), the lap completion percentage drops drastically, especially on Spa (12%) and Hockenheim (8%). As can be seen in Figure 4, both tracks contain sections with tight, technical turns, which expose a fundamental weakness of the policy: its limited ability to plan through sharp or blind corners. This is likely due to the reactive nature of its learned policy, which depends on immediate sensor inputs (e.g., LiDAR scans) without any map memory or long-term trajectory planning. As noted, successful navigation through sharp corners occasionally occurred when the agent inadvertently took wider lines into turns, allowing for better environmental visibility. However, this behavior appears to be incidental rather than intentional, underscoring the need for more diverse training environments or the integration of planning components into the policy.
This work explored the integration of imitation learning and reinforcement learning for autonomous racing on the F1TENTH platform. We aimed to surpass expert demonstration performance and improve upon previously laid-out work in the field. By bootstrapping PPO-based RL imitation policies, we observed that the resulting agent could outperform the easiest expert but struggled to beat the expert demonstrations. While the IL-RL framework significantly improved the sample efficiency by converging nearly three times faster than end-to-end RL, the final lap times plateaued regardless of the expert difficulty. Notably, end-to-end RL achieved the best lap times among learned policies and demonstrated commendable generalization to unseen tracks. However, the policy exhibited limitations in handling sharp or technical turns due to its reactive and memory-less design.
In summary, while IL pre-training accelerates RL convergence for autonomous racing, achieving performance surpassing experts may depend more critically on the RL algorithm's configuration and reward design. End-to-end RL, despite its sample inefficiency, showed potential for reaching a higher performance peak in this specific setup.
Future work can explore training the end-to-end RL policy on different maps and accounting for different types of turns an agent may encounter. Additionally, one could explore a different reward structure as we still felt there was ample room for improvement in performance. Secondly, we were curious to explore a curriculum learning approach using the expert demonstrations in order to more properly guide the policy towards peak performance. Due to time constraints, we were unable to explore these ideas and settled with simply tackling end-to-end RL and IL-RL.
Vineet Pasumarti: Responsible for implementing the HG-DAGGER imitation learning framework, including the expert demonstrator policies with varying difficulty levels and the human-gating mechanism. Developed the IL-RL integration pipeline and conducted the comparative analysis between bootstrapped and end-to-end approaches. Led the experimental design for multi-track generalization testing.
Ethan Senatore: Implemented the PPO reinforcement learning algorithm with hyperparameter tuning for both bootstrapped and end-to-end configurations. Designed the reward structure optimization through extensive experimentation with different reward weights and functions. Conducted training monitoring and analysis using Weights & Biases, identifying optimal convergence criteria.
- A. Kulkarni, J. Chrosniak, E. Ducote, F. Sauerbeck, A. Saba, U. Chirimar, J. Link, M. Behl, and M. Cellina, "Racecar - the dataset for high-speed autonomous racing," in 2023 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Oct. 2023, pp. 11458–11463, doi: 10.1109/iros55552.2023.10342053.
- B. D. Evans, R. Trumpp, M. Caccamo, F. Jahncke, J. Betz, H. W. Jordaan, and H. A. Engelbrecht, "Unifying f1tenth autonomous racing: Survey, methods and benchmarks," 2024. [Online]. Available: https://arxiv.org/abs/2402.18558
- E. Kaufmann, L. Bauersfeld, A. Loquercio, et al., "Champion-level drone racing using deep reinforcement learning," Nature, vol. 620, pp. 982–987, 2023, doi: 10.1038/s41586-023-06419-4.
- P. Koirala and C. Fleming, "F1tenth autonomous racing with offline reinforcement learning methods," 2024. [Online]. Available: https://arxiv.org/abs/2408.04198
- S. Ross, G. J. Gordon, and J. A. Bagnell, "A reduction of imitation learning and structured prediction to no-regret online learning," in Proceedings of the 14th International Conference on Artificial Intelligence and Statistics (AISTATS), vol. 15. PMLR, 2011, pp. 627–635.
- X. Sun, S. Yang, M. Zhou, K. Liu, and R. Mangharam, "Mega-dagger: Imitation learning with multiple imperfect experts," 2024. [Online]. Available: https://arxiv.org/abs/2303.00638
- X. Sun, M. Zhou, Z. Zhuang, S. Yang, J. Betz, and R. Mangharam, "A benchmark comparison of imitation learning-based control policies for autonomous racing," in 2023 IEEE Intelligent Vehicles Symposium (IV), 2023, pp. 1–5, doi: 10.1109/IV55152.2023.10186780.
- A. Heilmeier, A. Wischnewski, L. Hermansdorfer, J. Betz, M. Lienkamp, and B. Lohmann, "Minimum curvature trajectory planning and control for an autonomous race car," Vehicle System Dynamics, vol. 58, no. 10, pp. 1497–1527, 2019, doi: 10.1080/00423114.2019.1631455.